変分原理を用いた懸垂線の導出
はじめに
解析力学の授業で,変分原理というものに出会いました.「物理現象においてなにか(エネルギーなど)を最小にするように道が選ばれる」 という考えのことです.私たちは例えばコンビニに行こうとするときに,「この道は坂が急だから疲れそうだ」,「あの通りは歩きやすい」といったことを考えますよね. そうしてできるだけ労力をかけずにコンビニにたどり着こうとする,これも変分原理です.
目的
せっかく知識が身についたのだから,なにか応用してみたい.そこで,我々の日常生活にあふれている懸垂線(catenary)の関数を導出しよう!
懸垂線とはひもの二点を固定したときにできる曲線のことです.
導出過程
図のような懸垂線を導出していきます.ゴールは \(y\)を\(x\)の関数で表すことです. 重力加速度はy軸の負の向きにかかっていて,ひもの線密度は \(\rho\)とします.
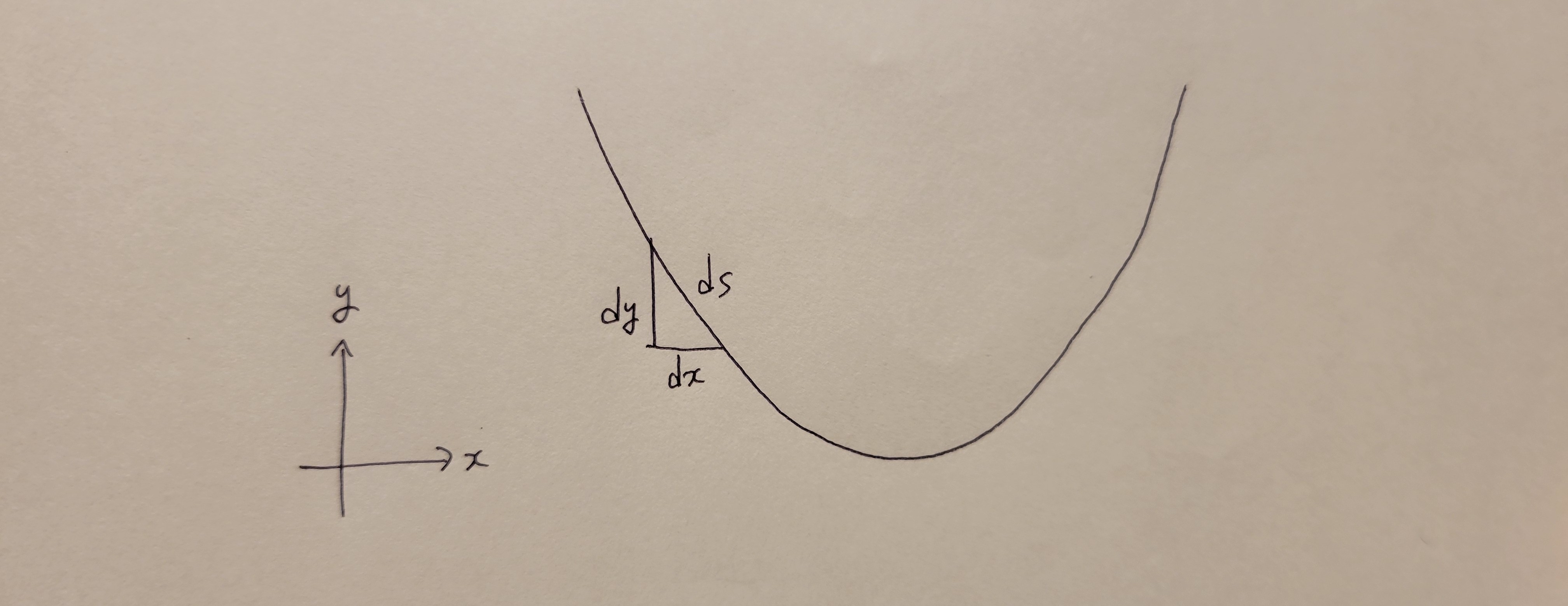
まず,図の微小部分に対して,三平方の定理より
\[\begin{align*} ds &= \sqrt{(dx)^2 + (dy)^2} \\ &= \sqrt{1 + y^{\prime 2}}dx \end{align*}\]ここで,微小部分のポテンシャルを出します.
\[\rho ds g y = \rho g y \sqrt{1 + y^{\prime 2}}\,dx\]ひも全体におけるポテンシャルを \(U\)とすると,\(y\)の汎関数として以下のようになりますね.
汎関数 \(U[y]\)が停留点をとる \(y(x)\)が今知りたい関数!
式\eqref{eq:potential}の被積分関数を \(F(y, y^{\prime})=\rho g y\sqrt{1 + y^{\prime 2}}\)とします.
ここで,オイラーの方程式により,
\[\begin{align*} \frac{d}{dx} \left(\frac{\partial F}{\partial y^{\prime}}\right) - \frac{\partial F}{\partial y} = 0 \\ \frac{d}{dx} \left(\frac{\rho g y y^{\prime}}{\sqrt{1+y^{\prime 2}}}\right) - \rho g\sqrt{1+y^{\prime 2}} = 0 \\ \end{align*}\]計算ミスに注意して,整理していきます.出来上がったものが式\eqref{eq:EOM}です.
これは非線形2階常微分方程式ですね!さあ,解いていきましょう.
式\eqref{eq:EOM}より
変数変換によって1階に落とすことができます.\(p=y^{\prime}\)とすると
\[y^{\prime \prime} = \frac{dp}{dx} = \frac{dp}{dy}\frac{dy}{dx} = p\frac{dp}{dy}\]式\eqref{eq:EOM2}に代入して変形していきます.
\[\begin{align*} y\left(p\frac{dp}{dy} \right) - p^2 = 1 \\ yp \frac{dp}{dy} = p^2 + 1\\ \frac{p}{p^2+1}dp = \frac{1}{y} dy \\ \end{align*}\]両辺積分して
\[\int\frac{p}{p^2+1}dp = \int\frac{1}{y} dy\]こうすると,積分定数をCやらDやらとして
\[\begin{align*} (\text{左辺}) &= \frac{1}{2} \ln|p^2+1| + C_1 \\ (\text{右辺}) &= \ln|y| + C_2 \\ \end{align*}\]したがって
\[\begin{align*} \frac{1}{2} \ln|p^2+1| &= \ln|y| + C_3 \\ (p^2+1)^{\frac{1}{2}} &= Cy \\ p^2+1 &= C^2 y^2 \end{align*}\]ここで \(p\)を戻してあげると
\[\begin{align*} \left(\frac{dy}{dx} \right)^2 &= C^2y^2 - 1 \\ \frac{dy}{dx} &= \sqrt{C^2 y^2 - 1} \\ \frac{dy}{\sqrt{C^2 y^2 - 1}} &= dx \\ \end{align*}\]両辺積分して
左辺について考えてみよう.じっとにらんでやると,2乗ひく2乗が1となる良い感じのものが欲しくなります.たちどころに
\[\cosh^2 y - \sinh^2 x = 1\]が頭に浮かぶであろう.\(Cy = \cosh u\)と置いてあげると \(dy = \frac{1}{C}\sinh u \,du\)のようにして変数変換をしていきますね.
\[\begin{align*} (\text{左辺}) &= \int \frac{\frac{1}{C} \sinh u}{\sqrt{\sinh^2 u}}du \\ &= \frac{1}{C}\int du \\ &= \frac{1}{C} u + C_4 \end{align*}\]ここで式\eqref{eq:int4}右辺は \(x+C_5\)になるから
\[\begin{align*} \frac{1}{C} u + C_4 &= x + C_5 \\ \frac{1}{C} u &= x + D \\ \frac{1}{C} \cosh^{-1} (Cy) &= x + D \\ y &= \frac{1}{C} \cosh (C(x + D)) \\ y &= \frac{1}{C} \cosh (Cx + b) \\ \end{align*}\]懸垂線はハイパボリックになることが導出できました! \(C\)やら \(b\)やらが含まれていますが,これは「ひもの全長」や「両端の座標」が与えられることで具体的に決まります.
まとめ
- 懸垂線を変分原理を用いて導出した!
- ハイパボリック関数で表されるなんて,本当に美しい