モールの応力円 Unityによる可視化

はじめに

応力の変換が理解できない！！！

材料力学を学ぶ一番の目的は，「材料のどこに，でかい力がかかっているのかを知ること」と先生がおっしゃっていました．

私はその第一歩がこの「応力の変換」だと感じています．

---

でも…

x方向，y方向の垂直応力, それらの面のせん断応力が与えられて，それをもとに，傾き \(\theta\) の面の垂直応力，せん断応力を求めろなんて言われても，頭の中で想像できない！

モールの応力円を作図すれば，主応力と最大せん断応力が求まると言われたけど，それぞれの角度においてモールの応力円と微小要素の関係性がわかりづらいですね．

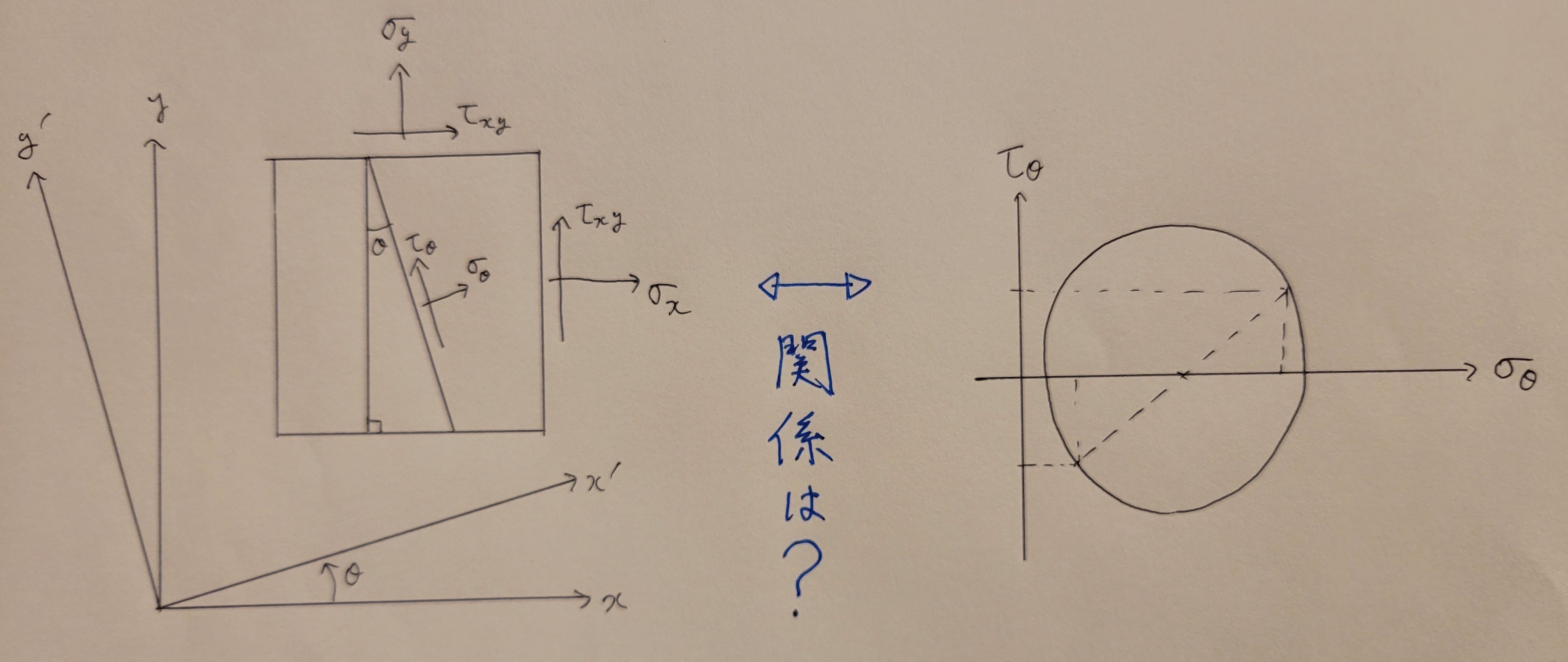
目的

上の図↑で任意の角度において，

• 垂直応力とせん断応力はどうなっているのか
• その点をモールの応力円にプロットしたら，どこに該当するのか

この2つを視覚的にとらえたい！

方法

Unityを用いて，再現してみた．

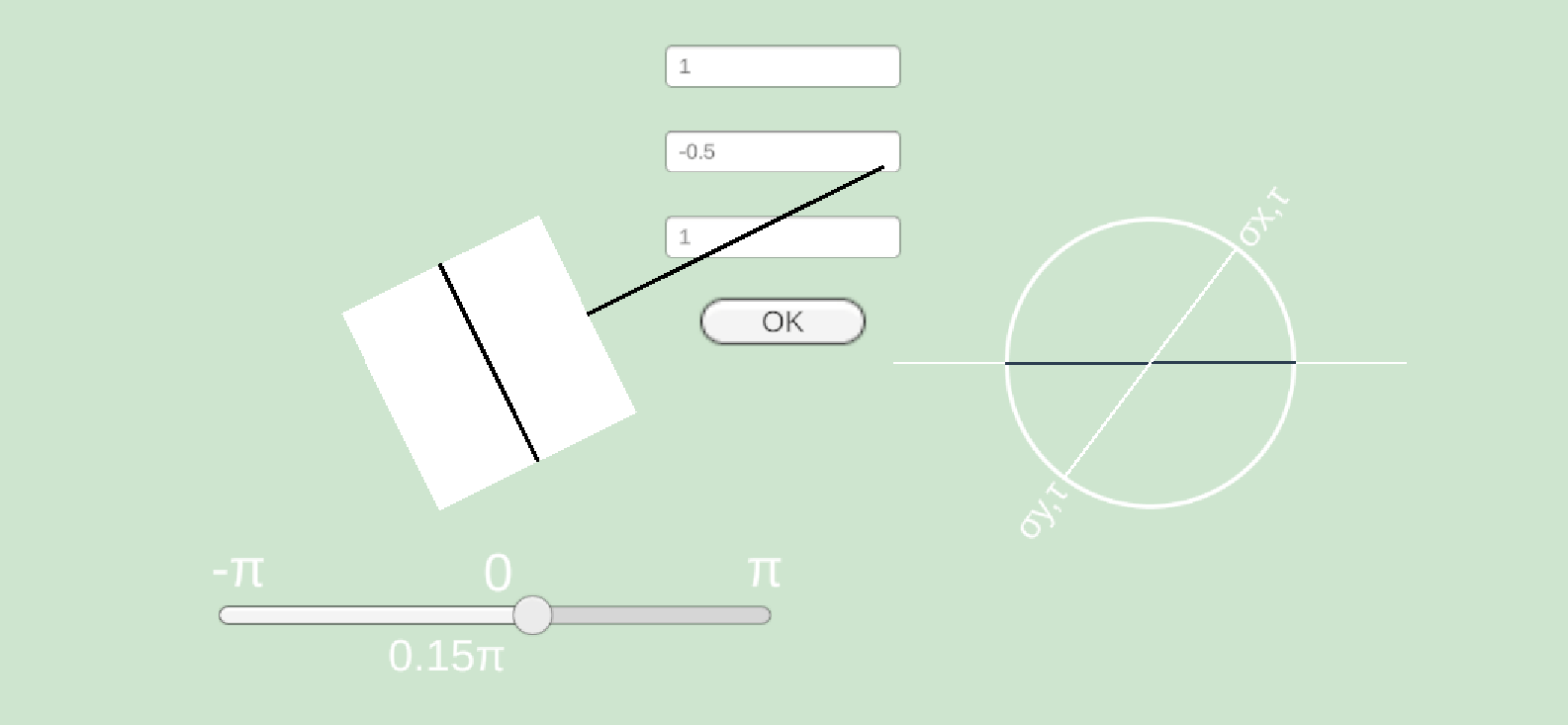
画面はこんな感じ．軸は最初の図と同じ．

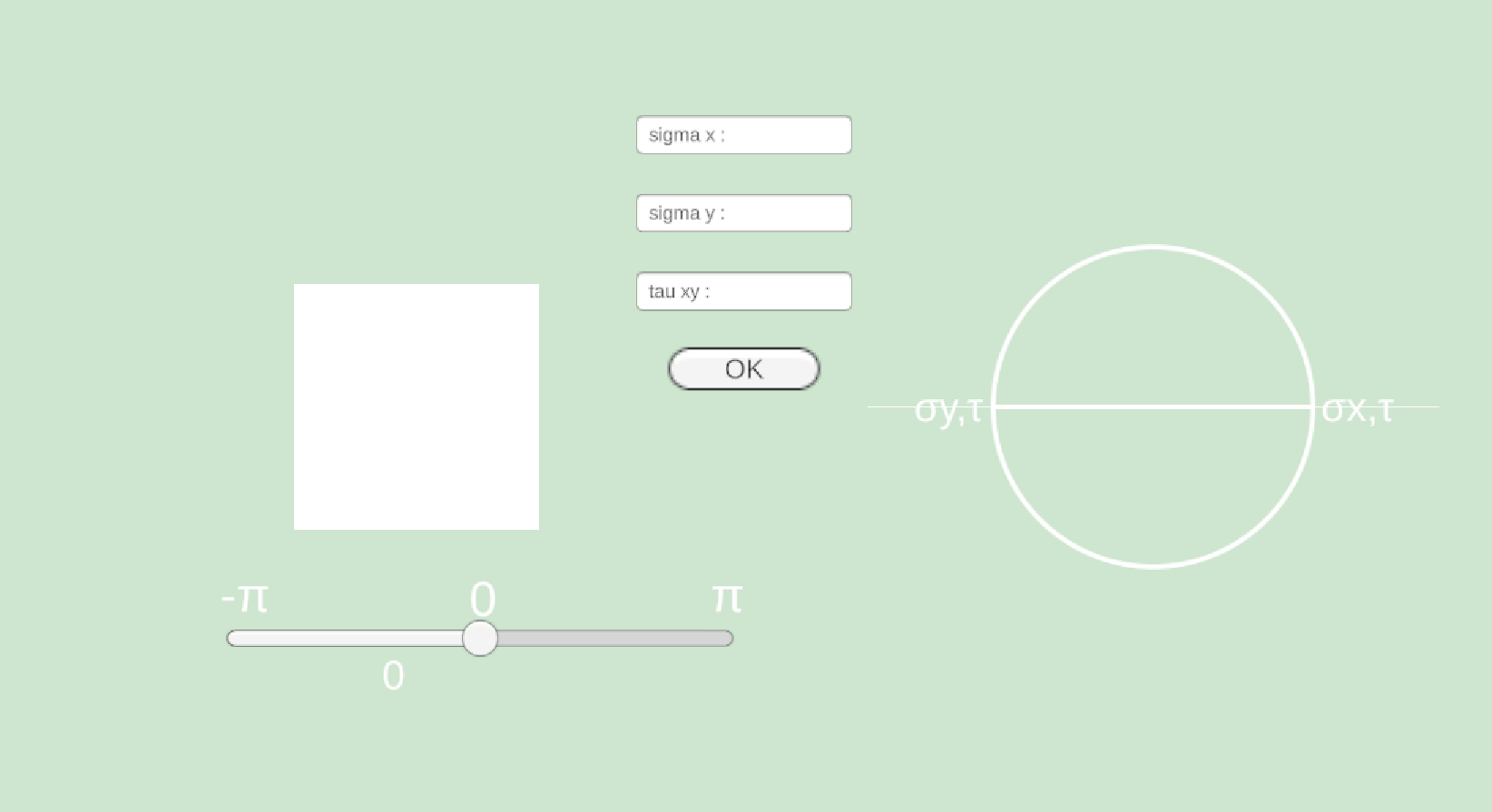
上から順番に，\(\sigma_x, \sigma_y, \tau_{xy}\) を入れてあげる．既知だからね．

黒の線が出現しましたが，これは大きさを表しています．（矢印にしたかったのですが，めんどくさくて棒に落ち着きました）

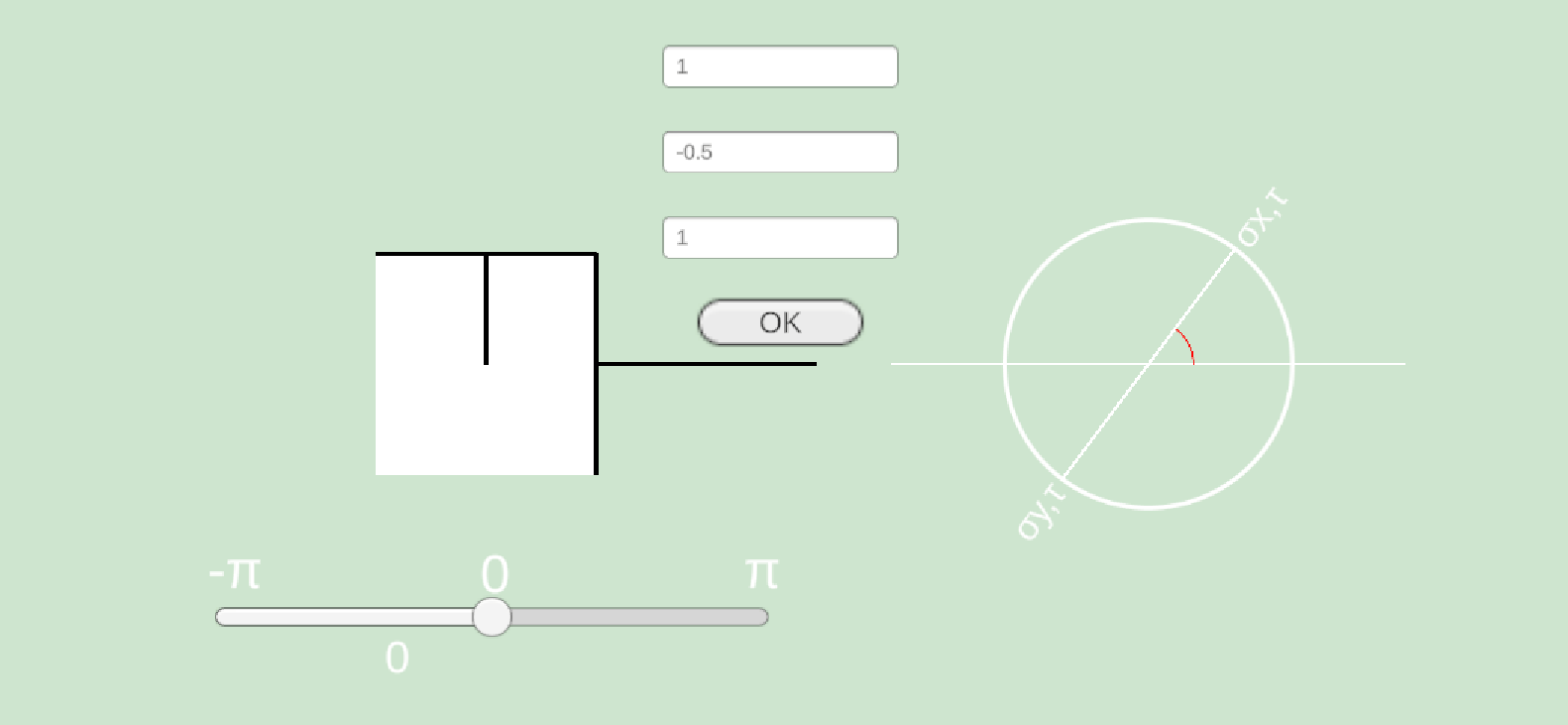
左下のスライドバーを動かすと微小要素が傾きます．それに伴って，モールの応力円上でどこにプロットされているのかが右の図に示されます．

ここで垂直応力を \(\sigma_{\theta}\), せん断応力を \(\tau_{\theta}\)とします．それぞれ以下の式で求められます．

\[\sigma_{\theta} = \frac{\sigma_x + \sigma_y}{2} + \frac{\sigma_x - \sigma_y}{2} \cos 2\theta + \tau_{xy} \sin 2\theta\] \[\tau_{\theta} = -\frac{\sigma_x - \sigma_y}{2} \sin 2\theta + \tau_{xy} \cos 2\theta\]

この式から，棒の長さを決めることができます．

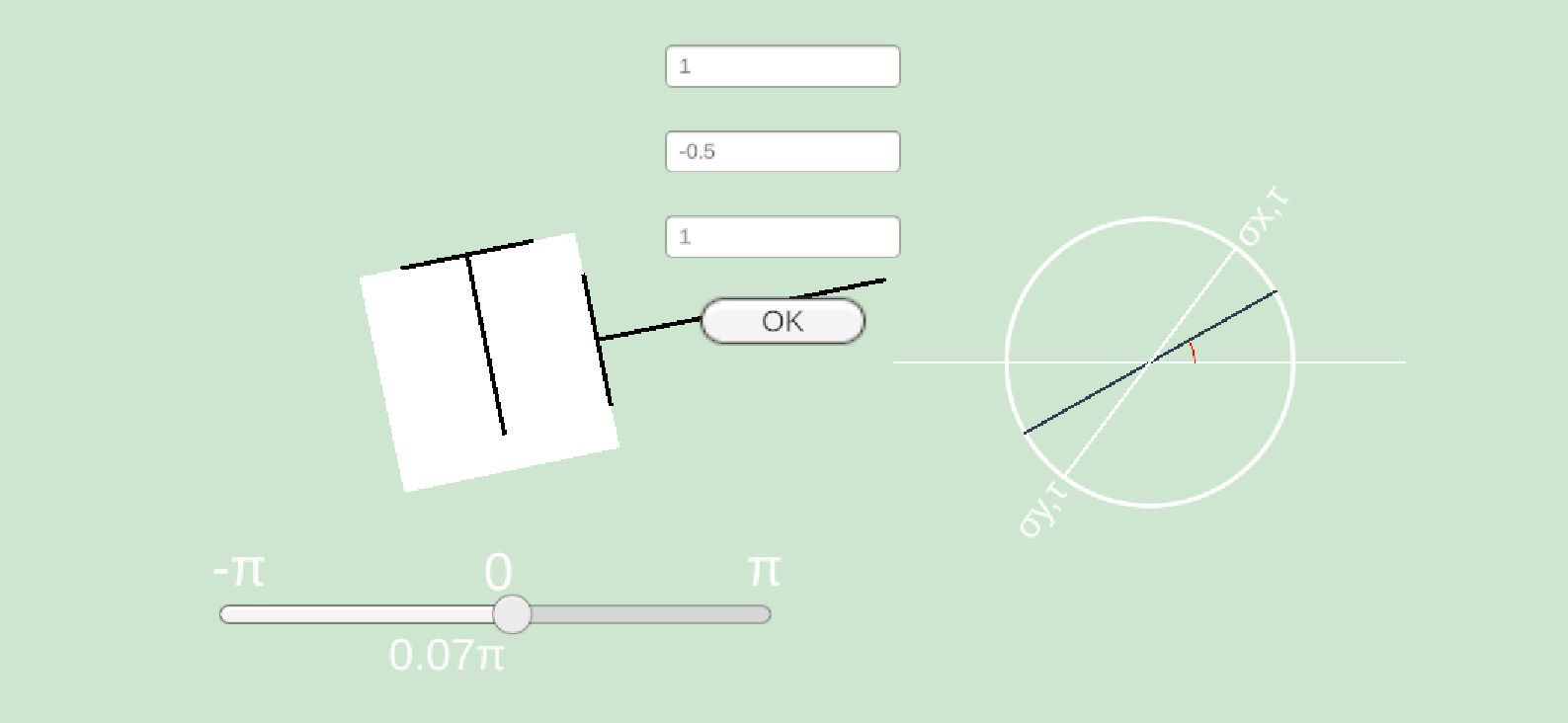
垂直応力が最大になるところを発見！！！これが主応力だー

いまからしたいこと

• 3次元に対応
• ひずみに関しても同様に作る
• UIをきれいにする

さいごに

このアプリを用いたら，少しは応力の変換が理解しやすくなるかも…